Vektorprodukt und Fläche
Zu zeigen:
$$
A = |\vec{a} \times \vec{b}| = |\vec{a}| \, |\vec{b}| \, sin(\gamma)
$$
Der Betrag des Vektorproduktes der Vektoren $\vec{a}$
und $\vec{b}$ ist gleich der Fläche des Parallelogramms,
welches von den beiden Vektoren $\vec{a}$ und $\vec{b}$
aufgespannt wird.
$$ A = |\vec{a} \times \vec{b}| $$
Bzw.:
$$ \vec{a} \times \vec{b} = |\vec{a}| \, |\vec{b}| \sin(\gamma) $$
($\gamma$ ist der von $\vec{a}$ und $\vec{b}$ eingeschlossene Winkel.)
Die Herleitung ist leider nicht elegant, sondern es wird
mit den einzelnen Komponenten der Vektoren
gerechnet und viele Terme langwierig
umgeformt. U. U. überspringen Sie bei einem
die Herleitung und kommen später darauf zurück.
Vorgehen
Bestimmen der Fläche des Parallelogramms mit Hilfe der Elementargeometrie: $A=g \cdot h$
Umformen des Terms der Flächenberechnung.
Umformen des Vektorproduktes und der Länge des Vektors.
Zeigen der Gleichheit der beiden Terme.
$$ A = |\vec{a}| \, |\vec{b}|\,\sin(\gamma) $$
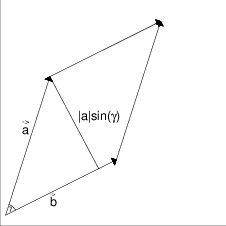
Als erstes bestimmen wir die Fläches des Parallelogramms.
Das Parallelogramm wird durch die Vektoren $\vec{a}$ und $\vec{b}$
aufgespannt.
$\gamma$ ist der durch
$\vec{a}$ und $\vec{b}$ eingeschlossene
Winkel.
Die Höhe steht senkrecht auf der Grundseite des Parallelogrammes.
Maxima Code
Da die Höhe senkrecht auf der Grundseite steht, gilt:
$$h = |\vec{a}|\,\sin(\gamma)$$
$|\vec{a}|$ ist die Länge der Hypotenuse, da die
Seite dem rechten Winkel gegenüberliegt.
Die Fläche eines Parallelogramms ist Grundseite mal Höhe:
$$
A = |\vec{b}| \, h
= |\vec{b}| \, |\vec{a}|\,\sin(\gamma)
= |\vec{a}| \, |\vec{b}|\,\sin(\gamma)
$$
$$ \frac{\vec{a} \cdot \vec{b}}{ |\vec{a}|\,|\vec{b}|} = \cos(\gamma)$$
$$\sin^2(\gamma) = 1 - \cos^2(\gamma)$$
$$
\sin(\gamma) = \sqrt{1 - \left(\frac{\vec{a} \cdot \vec{b}}{ |\vec{a}|\,|\vec{b}|} \right)^2}
$$
$$
A = |\vec{a}| \, |\vec{b}| \, \sqrt{1 - \left(\frac{\vec{a} \cdot \vec{b}}{ |\vec{a}|\,|\vec{b}|} \right)^2}
$$
In der Vektorrechnung haben wir bisher nur den Kosinus zur Verfügung:
Der Satz des Pyathagoras bietet die Verbindung zwischen dem Kosinus und dem Sinus eines Winkels:
$$
\begin{array}{rcl}
\sin^2(\gamma) + \cos^2(\gamma) &=& 1 \\
\sin^2(\gamma) &=& 1 - \cos^2(\gamma) \\
\sin(\gamma) &=& \sqrt{1 - \cos^2(\gamma)}
\end{array}
$$
$$ \vec{a} \cdot \vec{b} = |\vec{a}|\,|\vec{b}|\,\cos(\gamma)$$
$$ \frac{\vec{a} \cdot \vec{b}}{ |\vec{a}|\,|\vec{b}|} = \cos(\gamma)$$
Jetzt ersetzen wir $\cos(\gamma)$:
$$
\sin(\gamma) = \sqrt{1 - \left(\frac{\vec{a} \cdot \vec{b}}{ |\vec{a}|\,|\vec{b}|} \right)^2}
$$
Diesen Ausdruck setzen wir in die Formel für die Fläche ein:
$$
A = |\vec{a}| \, |\vec{b}|\, \sqrt{1 - \left(\frac{\vec{a} \cdot \vec{b}}{ |\vec{a}|\,|\vec{b}|} \right)^2}
$$
Dieser Ausdruck muss jetzt umgeformt werden bis die Gleichheit zum Vektorprodukt klar ist.
$$
A^2 = |\vec{a}|^2 \, |\vec{b}|^2 \left(1 - \left(\frac{\vec{a} \cdot \vec{b}}{ |\vec{a}|\,|\vec{b}|} \right)^2 \right)
$$
$$
A^2 = |\vec{a}|^2 \, |\vec{b}|^2 - \left(\vec{a} \cdot \vec{b} \right)^2
$$
Zuerst quadrieren wir beide Seiten, damit
der Ausdruck leichter lesbar ist, weil die Wurzel sich aufhebt:
$$
A^2 = |\vec{a}|^2 \, |\vec{b}|^2 \left (1 - \left(\frac{\vec{a} \cdot \vec{b}}{ |\vec{a}|\,|\vec{b}|} \right)^2 \right)
$$
Ausmultiplizieren der Klammer ergibt:
$$
A^2 = |\vec{a}|^2 \, |\vec{b}|^2 - \left(\vec{a} \cdot \vec{b} \right)^2
$$
$$
\begin{array}{rccl}
|\vec{a}|^2 \, |\vec{b}|^2
\\
&=&& a_1^2 b_1^2 + a_1^2 b_2^2 + a_1^2 b_3^2 \\
&&+& a_2^2 b_1^2 + a_2^2 b_2^2 + a_2^2 b_3^2 \\
&&+& a_3^2 b_1^2 + a_3^2 b_2^2 + a_3^2 b_3^2
\end{array}
$$
Nun rechnen wir mit den einzelnen Komponenten der Vektoren:
$$
\vec{a} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}
\,\,\,
\vec{b} = \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}
$$
Dies ergibt:
$$
|\vec{a}|^2 = a_1^2 + a_2^2 + a_3^2
$$
$$
|\vec{a}|^2 \, |\vec{b}|^2
=
(a_1^2 + a_2^2 + a_3^2) \cdot (b_1^2 + b_2^2 + b_3^2)
$$
Dies wird summandenweise ausmultipliziert:
$$
\begin{array}{rccl}
|\vec{a}|^2 \, |\vec{b}|^2
&=& &
(a_1^2 + a_2^2 + a_3^2) \cdot (b_1^2 + b_2^2 + b_3^2)
\\
&=&& a_1^2 b_1^2 + a_1^2 b_2^2 + a_1^2 b_3^2 \\
&&+& a_2^2 b_1^2 + a_2^2 b_2^2 + a_2^2 b_3^2 \\
&&+& a_3^2 b_1^2 + a_3^2 b_2^2 + a_3^2 b_3^2
\end{array}
$$
$$
\begin{array}{rccl}
(\vec{a} \cdot \vec{b})^2
&=&& (a_1 b_1)^2 + (a_2 b_2)^2 + (a_3 b_3)^2 \\
&&+& 2(a_1 a_2 b_1 b_2))
+ 2(a_1 a_3 b_1 b_3)
+ 2(a_2 a_3 b_2 b_3)
\end{array}
$$
Nun bestimmen wir komponentenweise $(\vec{a} \cdot \vec{b})^2$:
$$
\begin{array}{rccl}
(\vec{a} \cdot \vec{b})^2
&=& & (a_1 b_1 + a_2 b_2 + a_3 b_3)^2 \\
&=& & (a_1 b_1 + a_2 b_2 + a_3 b_3) \cdot (a_1 b_1 + a_2 b_2 + a_3 b_3)
\\
&=&& a_1 b_1 a_1 b_1 + \color{red}{a_1 b_1 a_2 b_2} + \color{green}{a_1 b_1 a_3 b_3} \\
&&+& \color{red}{a_2 b_2 a_1 b_1} + a_2 b_2 a_2 b_2 + \color{blue}{a_2 b_2 a_3 b_3} \\
&&+& \color{green}{a_3 b_3 a_1 b_1} + \color{blue}{a_3 b_3 a_2 b_2} + a_3 b_3 a_3 b_3 \\
\end{array}
$$
Gleichfarbige Summanden sind gleich groß. Umsortieren ergibt:
$$
\begin{array}{rccl}
(\vec{a} \cdot \vec{b})^2
&=&& (a_1 b_1)^2 + (a_2 b_2)^2 + (a_3 b_3)^2 \\
&&+& 2(\color{red}{a_1 a_2 b_1 b_2)})
+ 2(\color{green}{a_1 a_3 b_1 b_3})
+ 2(\color{blue}{a_2 a_3 b_2 b_3})
\end{array}
$$
Jetzt sammeln wir alle Terme:
$$
\begin{array}{rccl}
A^2 &=&& |\vec{a}|^2 \, |\vec{b}|^2 - (\vec{a} \cdot \vec{b})^2 \\
|\vec{a}|^2 \, |\vec{b}|^2
&=& & (a_1 b_1)^2 + (a_1 b_2)^2 + (a_1 b_3)^2 \\
&&+& (a_2 b_1)^2 + (a_2 b_2)^2 + (a_2 b_3)^2 \\
&&+& (a_3 b_1)^2 + (a_3 b_2)^2 + (a_3 b_3)^2 \\
(\vec{a} \cdot \vec{b})^2
&=& & (a_1 b_1)^2 + (a_2 b_2)^2 + (a_3 b_3)^2 \\
&&+& 2(a_1 a_2 b_1 b_2)
+ 2(a_1 a_3 b_1 b_3) + 2(a_2 a_3 b_2 b_3)
\end{array}
$$
Im nächsten Schritt werden wir diese Terme in $A^2$ einsetzen und dann zusammenfassen.
$$
\begin{array}{rcl}
A^2
=&& a_1^2 b_2^2 + a_1^2 b_3^2 + a_2^2 b_1^2 + a_2^2 b_3^2 + a_3^2 b_1^2 + a_3^2 b_2^2 \\
&-& 2(a_1 a_2 b_1 b_2) - 2(a_1 a_3 b_1 b_3) - 2(a_2 a_3 b_2 b_3)
\end{array}
$$
$$
\begin{array}{rccl}
A^2 &=&& |\vec{a}|^2 \, |\vec{b}|^2 - (\vec{a} \cdot \vec{b})^2 \\
&=&& \color{red}{(a_1 b_1)^2} + (a_1 b_2)^2 + (a_1 b_3)^2 \\
&&+& (a_2 b_1)^2 + \color{green}{(a_2 b_2)^2} + (a_2 b_3)^2 \\
&&+& (a_3 b_1)^2 + (a_3 b_2)^2 + \color{blue}{(a_3 b_3)^2} \\
&&-& \left (\color{red}{(a_1 b_1)^2} + \color{green}{(a_2 b_2)^2} + \color{blue}{(a_3 b_3)^2} \right) \\
&&-& \left ( 2(a_1 a_2 b_1 b_2)
+ 2(a_1 a_3 b_1 b_3) + 2(a_2 a_3 b_2 b_3) \right)
\end{array}
$$
Gleichfarbige Summanden sind gleich groß. Vereinfachen
(Herausstreichen der farbigen Summanden und Auflösen der Klammer)
führt zu folgendem Term:
$$
\begin{array}{rccl}
A^2 &=&& |\vec{a}|^2 \, |\vec{b}|^2 - (\vec{a} \cdot \vec{b})^2 \\
&=&& a_1^2 b_2^2 + a_1^2 b_3^2 \\
&&+& a_2^2 b_1^2 + a_2^2 b_3^2 \\
&&+& a_3^2 b_1^2 + a_3^2 b_2^2 \\
&&-& 2(a_1 a_2 b_1 b_2) - 2(a_1 a_3 b_1 b_3) - 2(a_2 a_3 b_2 b_3)
\end{array}
$$
Bzw. in zwei Zeilen:
$$
\begin{array}{rcl}
A^2
=&& a_1^2 b_2^2 + a_1^2 b_3^2 + a_2^2 b_1^2 + a_2^2 b_3^2 + a_3^2 b_1^2 + a_3^2 b_2^2 \\
&-& 2(a_1 a_2 b_1 b_2) - 2(a_1 a_3 b_1 b_3) - 2(a_2 a_3 b_2 b_3)
\end{array}
$$
$$
\begin{array}{rcl}
|\vec{a} \times \vec{b}|^2
&=& (a_2 b_3)^2 - 2 a_2 a_3 b_2 b_3 + (a_3 b_2)^2 \\
&+& (a_3 b_1)^2 - 2 a_1 a_3 b_1 b_3 + (a_1 b_3)^2 \\
&+& (a_1 b_2)^2 - 2 a_1 a_2 b_1 b_2 + (a_2 b_1)^2
\end{array}
$$
Nun untersuchen wir das Vektorprodukt.
$$
\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}
\times
\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}
=
\begin{pmatrix}
a_2 b_3 - a_2 b_2 \\
a_3 b_1 - a_1 b_3 \\
a_1 b_2 - a_2 b_1
\end{pmatrix}
$$
Nun bestimmen wir das Quadrat des Betrages des Vektorproduktes.
Für die Umformungen verwenden wir die binomischen Formeln.
$$
\begin{array}{rcl}
|\vec{a} \times \vec{b}|^2
&=& (a_2 b_3 - a_3 b_2)^2 + (a_3 b_1 - a_1 b_3)^2 + (a_1 b_2 - a_2 b_1)^2 \\
&=& (a_2 b_3)^2 - 2 a_2 b_3 a_3 b_2 + (a_3 b_2)^2 \\
&+& (a_3 b_1)^2 - 2 a_3 b_1 a_1 b_3 + (a_1 b_3)^2 \\
&+& (a_1 b_2)^2 - 2 a_1 b_2 a_2 b_1 + (a_2 b_1)^2
\end{array}
$$
Sortieren nach Buchstaben und Indizes in den einzelnen Summanden:
$$
\begin{array}{rcl}
|\vec{a} \times \vec{b}|^2
&=& (a_2 b_3)^2 - 2 a_2 a_3 b_2 b_3 + (a_3 b_2)^2 \\
&+& (a_3 b_1)^2 - 2 a_1 a_3 b_1 b_3 + (a_1 b_3)^2 \\
&+& (a_1 b_2)^2 - 2 a_1 a_2 b_1 b_2 + (a_2 b_1)^2
\end{array}
$$
Ein Vergleich ergibt, dass die beiden Terme identisch sind.
Gleiche Summanden haben dieselbe Farbe.
$$
\begin{array}{rl}
A^2 =
& \color{red}{(a_1 b_2)^2}
+ \color{green} {(a_1 b_3)^2}
+ \color{blue} {(a_2 b_1)^2}
+ \color{violet} {(a_2 b_3)^2}
+ \color{brown} {(a_3 b_1)^2}
+ \color{cyan} {(a_3 b_2)^2} \\
& - \color{magenta} {2(a_1 a_2 b_1 b_2)}
- \color{purple} {2(a_1 a_3 b_1 b_3)}
- \color{orange} {2(a_2 a_3 b_2 b_3)}
\end{array}
$$
$$
\begin{array}{rcl}
|\vec{a} \times \vec{b}|^2
&=& \color{violet} {(a_2 b_3)^2}
- \color{orange} {2 a_2 a_3 b_2 b_3}
+ \color{cyan} {(a_3 b_2)^2} \\
&+& \color{brown} {(a_3 b_1)^2}
- \color{purple} {2 a_1 a_3 b_1 b_3}
+ \color{green} {(a_1 b_3)^2} \\
&+& \color{red} {(a_1 b_2)^2}
- \color{magenta}{2 a_1 a_2 b_1 b_2}
+ \color{blue} {(a_2 b_1)^2}
\end{array}
$$
Insbesondere gilt dann auch in Anlehnung an das Skalarprodukt:
$$
\vec{a} \times \vec{b} = |\vec{a}| \, |\vec{b}| \, \sin(\gamma)
$$
Ein Vergleich ergibt, dass die beiden Terme identisch sind.
Gleiche Summanden haben dieselbe Farbe.
$$
\begin{array}{rl}
A^2 =
& \color{red}{(a_1 b_2)^2}
+ \color{green} {(a_1 b_3)^2}
+ \color{blue} {(a_2 b_1)^2}
+ \color{violet} {(a_2 b_3)^2}
+ \color{brown} {(a_3 b_1)^2}
+ \color{cyan} {(a_3 b_2)^2} \\
& - \color{magenta} {2(a_1 a_2 b_1 b_2)}
- \color{purple} {2(a_1 a_3 b_1 b_3)}
- \color{orange} {2(a_2 a_3 b_2 b_3)}
\end{array}
$$
$$
\begin{array}{rcl}
|\vec{a} \times \vec{b}|^2
&=& \color{violet} {(a_2 b_3)^2}
- \color{orange} {2 a_2 a_3 b_2 b_3}
+ \color{cyan} {(a_3 b_2)^2} \\
&+& \color{brown} {(a_3 b_1)^2}
- \color{purple} {2 a_1 a_3 b_1 b_3}
+ \color{green} {(a_1 b_3)^2} \\
&+& \color{red} {(a_1 b_2)^2}
- \color{magenta}{2 a_1 a_2 b_1 b_2}
+ \color{blue} {(a_2 b_1)^2}
\end{array}
$$
Insbesondere gilt dann auch in Anlehnung an das Skalarprodukt:
$$
\vec{a} \times \vec{b} = |\vec{a}| \, |\vec{b}| \, \sin(\gamma)
$$


 Koordinatensystem
Koordinatensystem