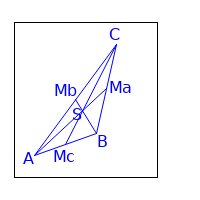
Schnittpunkt der Seitenhalbierenden im Dreieck
(Eigenschaften von Vektoren und deren Vielfache) (Beweis durch Schnittpunkt von Geraden hier)In diesem Abschnitt beschäftigen wir uns mit dem Schnittpunkt der Seitenhalbierenden eines Dreiecks. Wir werden zwei Eigenschaften beweisen:
- Die Seitenhalbierenden schneiden sich alle in einem gemeinsamen Punkt S.
- Der Punkt S teilt jede Seitenhalbierende im Verhältnis 2:1. Wobei die längere Strecke die Strecke von der Ecke bis zum Punkt S ist.
Seitenhalbierende sind Linien im Dreieck. Sie verbinden die Eckpunkte eines Dreiecks mit der Mitte der gegenüberliegenden Seite.
In diesem Beweis benötigen wir nur die Eigenschaften von Vektoren und deren Vielfachen. Hier gibt es einen anderen Beweis, der den Schnittpunkt S der Seitenhalbierenden als Schnittpunkt von Geraden ermittelt.
Maxima Code
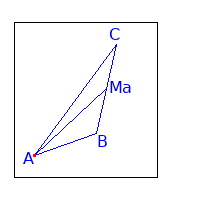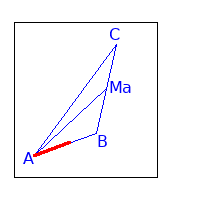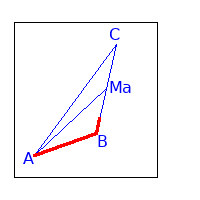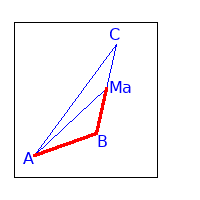
- Wir legen den Punkt A als Ausgangspunkt (Koordinatenursprung) fest.
- Wir legen den Punkt S fest.
- Wir bestimmen den Pfad von A zu Ma: sa
- Wir zeigen dann, dass S ein Punkt von sa ist.
- Dann zeigen wir dass S ein Punkt von sb ist.
- Anschließend zeigen wir dass S ein Punkt von sc ist.
S ist ein Punkt, den alle drei Seitenhalbierenden besitzen. ⇒ S ist ein gemeinsamer Punkt aller Seitenhalbierenden. Also ist S der Schnittpunkt der drei Seitenhalbierenden.
Festlegen des Koordinatenursprunges
A sei der Koordinatenurpsrung.S angeben
$$ S = \frac{1}{3} \overrightarrow{AB} + \frac{1}{3} \overrightarrow{AC} $$ Dies bedeutet, dass wir im folgenden immer alle Vektoren durch $\overrightarrow{AB}$ und $\overrightarrow{AC}$ beschreiben werden.S als Teilpunkt von sa
Maxima Code
$$ \overrightarrow{AM_a} = \overrightarrow{AB} + \frac{1}{2} \overrightarrow{BC} $$ Da wir den Punkt S mit den Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AC}$ beschrieben haben, werden wir $\overrightarrow{BC}$ durch $\overrightarrow{AB}$ und $\overrightarrow{AC}$ ersetzen: $$ \overrightarrow{BC} = -\, \overrightarrow{AB} + \overrightarrow{AC} $$ wenn wir diese Gleichungen zusammenführen erhalten wir: $$ \begin{array}{rcl} \overrightarrow{AM_a} &=& \overrightarrow{AB} + \frac{1}{2} \overrightarrow{BC} \\ &=& \overrightarrow{AB} + \frac{1}{2} (-\, \overrightarrow{AB} + \overrightarrow{AC}) \\ &=& \frac{1}{2} \overrightarrow{AB} + \frac{1}{2} \overrightarrow{AC} \\ \end{array} $$ Nun zeigen wir, dass der Punkt S ein Teil von sa ist: $$ \begin{array}{rcl} \frac{2}{3} \overrightarrow{AM_a} &=& \frac{2}{3} \cdot \frac{1}{2} \overrightarrow{AB} + \frac{2}{3} \cdot \frac{1}{2} \overrightarrow{AC} \\ &=& \frac{1}{3} \overrightarrow{AB} + \frac{1}{3} \overrightarrow{AC} \\ &=& S \end{array} $$
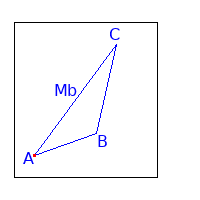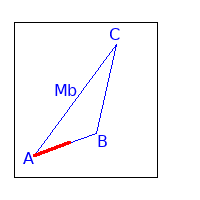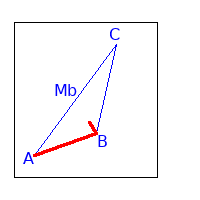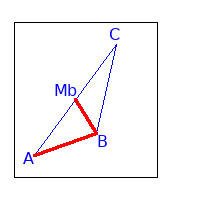
S als Teilpunkt von sb
Maxima Code
Wir wollen folgendes zeigen: $$ S = \overrightarrow{AB} + \frac{2}{3} \overrightarrow{BM_b} $$
Da wir ja mit unserem gegebenen Punkt vergleichen wollen, den wir nur mit $\overrightarrow{AB}$ und $\overrightarrow{AC}$ ausgedrückt haben, müssen wir $\overrightarrow{BM_b}$ ersetzen durch einen anderen Vektorpfad.
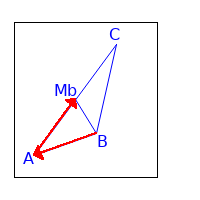
Der Pfad von B über A zu Mb kann geschrieben werden durch: $\overrightarrow{BM_b} = -\, \overrightarrow{AB} + \frac{1}{2} \overrightarrow{AC}$
Maxima Code
Einsetzen ergibt: $$ \begin{array}{rcl} \overrightarrow{AB} + \frac{2}{3} \overrightarrow{BM_b} &=& \overrightarrow{AB} + \frac{2}{3} (-\, \overrightarrow{AB} + \frac{1}{2} \overrightarrow{AC}) \\ &=& \overrightarrow{AB} - \frac{2}{3} \overrightarrow{AB} + \frac{2}{3} \cdot \frac{1}{2} \overrightarrow{AC} \\ &=& \frac{1}{3} \overrightarrow{AB} + \frac{1}{3} \overrightarrow{AC} \\ &=& S \end{array} $$
S als Teilpunkt von sc
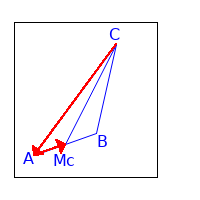
Maxima Code
Beweisende
Da S ein Punkt von allen drei Seitenhalbierenden ist, muss S der Schnittpunkt aller drei Seitenhalbierenden sein.
Darüber hinaus teilt der Punkt S jede Seitenhalbierende im Verhältnis 2:1.

 Koordinatensystem
Koordinatensystem