Koordinatensystem
Geometrische Definition
Ein Vektor kann geometrisch zwei Bedeutungen haben:
- er beschreibt einen Punkt
- er beschreibt eine Verschiebung eines Punktes
Wenn zwei Punkte in einem Koordinatensystem vorhanden sind, dann kann der Vektor angeben, um welche Werte in x-Richtung und y-Richtung (evtl. z-Richtung) der Punkt A verschoben werden muss, damit er auf dem Punkt B liegt.
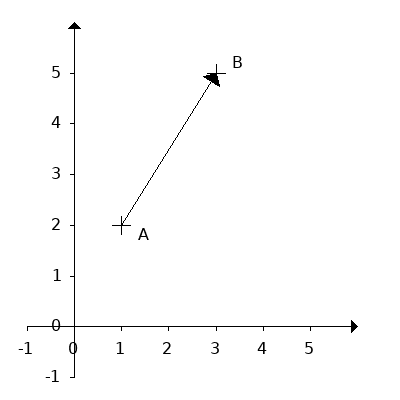
Die x-Komponente und die y-Koopmonente und gegebenenfalls die z-Komponente werden untereinander geschrieben. Um vom Punkt A zum Punkt B zu gelangen, muss man den Punkt A um ...
- 2 Einheiten in die x-Richtung bewegen
- 3 Einheiten in die y-Richtung bewegen
$$ A + \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} + \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 3 \\ 5 \end{pmatrix} = B $$
Verschiebungsvektoren kann man sich als Pfeile veranschaulichen.
Sie haben dann eine Richtung und eine Länge.
Dabei gilt:
Parallele Pfeile mit derselben Länge beschreiben dieselbe Verschiebung
und damit denselben Vektor.
Vektoren werden hier in der Lernumgebung mit Kleinbuchstaben und durch einen Pfeil gekennzeichnet. Dies erleichtert das Lesen. Dann müssen wir nicht jedesmal aufschreiben, welche der Variablen ein Vektor und welche Variable eine Zahl darstellen soll.
| $\overrightarrow{a}$: | Dies steht für einen Vektor. |
| $r$: | Dies steht für eine Zahl . |
- Fettdruck: a
- Unterstrichen: a
- in alten Büchern werden Vektoren in Süterlin geschreiben.
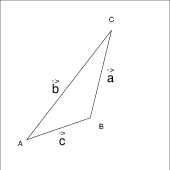
Wenn Sie in A starten und um das Dreieck herumgehen, sind Sie wieder bei A. Dann haben Sie sich nicht bewegt. Mit dieser Hilfe können Sie im Dreieck einen Vektor durch zwei andere Ausdrücken. Beachten Sie die jeweilige Richtung der Vektoren. $$ \begin{array}{rcl} \overrightarrow{a} &=& B-A\\ \overrightarrow{b} &=& C-A\\ \overrightarrow{c} &=& C-B\\ \end{array} $$ $$ \begin{array}{rcl} \overrightarrow{c} + \overrightarrow{a} - \overrightarrow{b} &=& 0 \\ \overrightarrow{a} &=& \overrightarrow{b} - \overrightarrow{c} \end{array} $$