Die Normalenform

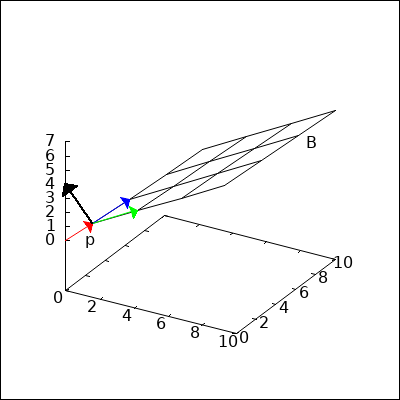
Eine Ebene und ihre Normale.
Der Normalenvektor (schwarz) ist senkrecht zur Ebene. Jede Linie in der Ebene ist senkrecht zum Normelenvektor der Ebene. Maxima Code

Der Vektor $\overrightarrow{pB}$ ist für jeden beliebigen Punkt B senkrecht zum Normalenvektor. Also ist das Skalarprodukt des Vektors mit dem Normalenvektor null. $$ E: [\vec{x} - \vec{p} ] \cdot \vec{n} = 0 $$ $\vec{p}$ ist ein gegebener Punkt der Ebene.
$\vec{x}$ ist ein weiterer Punkt der Ebene.
$\vec{x} - \vec{A}$ ist parallel zur Ebene und damit senkrecht zum Normalenvektor.
Das Skalarprodukt ergibt null, weil die beiden Vektoren senkrecht zu einander sind.
Alle Punkte $\vec{x}$, die diese Gleichung erfüllen sind Punkte der Ebene.

Erstellen der Normalenform aus der Parameterform

Der Normalenvektor wird mit Hilfe des Vektorproduktes aus den Richtungsvektoren gebildet: $$ E: \vec{x} = A + r \vec{u} + s \vec{v} $$ $$ \vec{n} = \vec{u} \times \vec{v} $$

Beispiel: Gegeben ist die folgende Ebene: $$ E: \vec{x} = \begin{pmatrix} 1\\2\\3 \end{pmatrix} + r \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + s \begin{pmatrix} 2 \\ 3 \\ 0 \end{pmatrix} $$ Der Normalenvektor ergibt sich als Kreuzprodukt aus den Richtungsvektoren: $$ \begin{array}{rcl} \vec{n} &=& \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \times \begin{pmatrix} 2 \\ 3 \\ 0 \end{pmatrix} \\ &=& \begin{pmatrix} -3 \\ 2 \\ -1 \end{pmatrix} \end{array} $$ Dann ergibt sich die Normalenform zu: $$ E: \left[ \vec{x} - \begin{pmatrix} 1\\2\\3 \end{pmatrix} \right] \cdot \begin{pmatrix} -3 \\ 2 \\ -1 \end{pmatrix} = 0 $$

Hinweise zur Normalenform

  1. Im Prinzip überprüfen Sie für jeden Punkt $\vec{x}$ im Raum ob dieser Punkt die Bedingung der Normalengleichung erfüllt und somit ein Punkt der Ebene ist.
  2. Es kommt nur auf die Richtung des Normalenvektors an. Also ist es in der Regel sinnvoll die Länge des Normalenvektors so zu wählen, dass Sie ganze Zahlen und möglichst kleine Zahlen haben. Dazu multiplizieren Sie dass Vektorprodukt mit einer beliebigen (auch negativen) Zahl.
  3. Ob zwei Ebenen gleich sind, ist hier leicht zu ermitteln.
    • Sie müssen überprüfen, ob der Punkt der zweiten Ebene in der ersten Ebene enthalten ist. (Punktprobe) Dazu setzen Sie den Punkt der zweiten Ebene in die Normalengleichung der ersten Ebene ein.
    • Sie müssen überprüfen, ob die Normalenvektoren Vielfache voneinander sind.