Die Länge eines Vektors im euklidischen Koordinatensystem

Die Länge des Vektors wird durch zwei senkrechte Striche um den Vektor angegeben: $|\overrightarrow{a}|$. Man sagt z. B.: "Die Länge des Vektors $|\overrightarrow{a}|$ ist 3" oder auch: "Der Betrag des Vektors $|\overrightarrow{a}|$ ist 3."

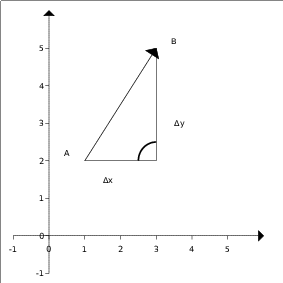
Ein Vektor als Hypotenuse im rechtwinkligen Dreieck. — Ein Vektor ist die Hypotenuse im rechtwinkligen Dreieck, bei kartesischen Koordinaten. $\delta y = y_2 - y_1$ und $\delta x = x_2 - x_1$. Maxima Code

Hier ist ein kartesiches Koordinatensystem vorhanden bei dem die Achsen im 90° Winkel zueinander stehen. Der Pfeil kann dann als Hypotenuse im rechtwinkligen Dreieck gedeutet werden. $$\Delta x = B_x - A_x = 3 - 1 = 2$$ $$\Delta y = B_y - A_y = 5 - 2 = 3$$ $$\overrightarrow{AB} = \begin{pmatrix} 2\\3 \end{pmatrix} $$ $$|\overrightarrow{AB}| = \sqrt{2^2 + 3^2} = \sqrt{13} $$ Die Länge des Pfeils in der obigen Graphik ist $ \sqrt{13} $.

Ein weiteres Beispiel

$$ \overrightarrow{a} = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \,\, |\overrightarrow{a}| = \sqrt{a_1^2 + a_2^2} $$ $$ \overrightarrow{a} = \begin{pmatrix} 6 \\ 8 \end{pmatrix} \,\, |\overrightarrow{a}| = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = 10 $$ Entsprechend in drei Dimensionen: $$ \overrightarrow{b} = \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} \,\, |\overrightarrow{b}| = \sqrt{b_1^2 + b_2^2 + b_3^2} $$ $$ \overrightarrow{b} = \begin{pmatrix} 1 \\ 8 \\ 4 \end{pmatrix} \,\, |\overrightarrow{b}| = \sqrt{1^2 + 8^2 + 4^2} = \sqrt{1 + 64 + 16} = 9 $$