Ebene in Parameterdarstellung

Die Parameterform

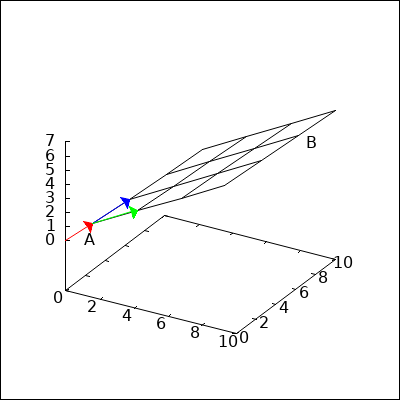
Eine Ebene.
In diesem Bild sehen Sie wie jeder Punkt der Ebene durch die drei Vektoren gebildet werden kann. Vom Punkt A aus gehen Sie Vielfache der beiden Richtungsvektoren. So wird z. B. der Punkt B von Punkt A aus durch Ansetzen von drei mal dem grünen Vektor und zwei mal dem blauen Vektor gebildet: $$B = A + 3 \cdot \overrightarrow{v_g} + 2 \cdot \overrightarrow{v_b}$$ Maxima Code

Eine Ebene in Parameterform wird durch einen Punkt und zwei Vektoren angegeben. $$ E: \overrightarrow{x} = A + r \overrightarrow{u} + s \overrightarrow{v} $$ $A$ ist der Punkt. Die beiden Vektoren $\overrightarrow{u}$ und $\overrightarrow{v}$ nennt man Richtungsvektoren. Vielfache dieser Richtungsvektoren werden zum Punkt addiert.

Erstellen der Ebenengleichung aus drei Punkten

Die Richtungsvektoren ergeben sich aus der Differenz zweier Punkte.

Beispiel: Gegeben sind drei Punkte der Ebene: A(1|2|3), B (2|4|2) und C(3|5|3).
Als mögliche Richtungsvektoren lassen sich bestimmen: $$ \begin{array} \overrightarrow{u} = B-A = \begin{pmatrix} 2\\4\\2 \end{pmatrix} - \begin{pmatrix} 1\\2\\3 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \\ \overrightarrow{v} = C-A = \begin{pmatrix} 3 \\ 5 \\ 3 \end{pmatrix} - \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \\ 0 \end{pmatrix} \\ \overrightarrow{w} = C-B = \begin{pmatrix} 3 \\ 5 \\ 3 \end{pmatrix} - \begin{pmatrix} 1\\2\\3 \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \\ 0 \end{pmatrix} \end{array} $$ Sie benötigen nur zwei Richtungsvektoren. Einen der Punkte müssen Sie angeben. $$ E_1: \overrightarrow{x} = \begin{pmatrix} 1\\2\\3 \end{pmatrix} + r \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} + s \begin{pmatrix} 2 \\ 3 \\ 0 \end{pmatrix} $$ Da es bei den Richtungsvektoren nur auf die Richtung ankommt, können Sie auch Vielfache der Vektoren wählen oder Kombinationen aus den Richtungsvektoren. $$ E_2: \overrightarrow{x} = \begin{pmatrix} 1\\2\\3 \end{pmatrix} + r \begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} + s \begin{pmatrix} 3 \\ 5 \\ 1 \end{pmatrix} $$ $E_1$ und $E_2$ sind dieselbe Ebene. Bei $E_2$ ist der erste Richtungsvektor das Doppelte des ersten Richtungsvektors von $E_1$. Der zweite Richtungsvektor ist die Summe der beiden Richtungsvektoren von $E_1$.

Hinweise zur Parameterform

  1. Die Parameterform erzeugt alle Punkte der Ebene direkt. Sie werden später noch Formen kennenlernen, bei denen nur überprüft werden kann, ob ein Punkt ein Punkt der Ebene ist.
  2. Die Richtungsvektoren dürfen nicht parallel sein. D. h. nicht Vielfache voneinander sein. Sonst erhalten Sie nur eine Gerade
  3. Ob zwei Ebenen gleich sind, ist dagegen schwierig zu ermitteln.
    • Sie müssen überprüfen, ob der Punkt der zweiten Ebene in der ersten Ebene enthalten ist. (Punktprobe)
    • Sie müssen überprüfen, ob die Richtungsvektoren der zweiten Ebene sich durch die Richtungsvektoren der ersten Ebene darstellen lassen. (Lineare Abhängigkeit)