Koordinatensystem
Abstand zwischen einem Punkt und einer Geraden: Flächenvergleich
Gesucht ist der minimale Abstand zwischen einem
Punkt und einer Geraden.
$$
g: \vec{x} = \vec{a} + t \vec{v}
\;\;\;
P = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix}
$$
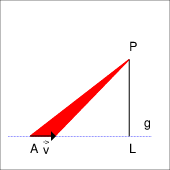
Die Grundseite des Dreiecks habe die Länge 1. Wir bestimmen die Fläche des roten Dreiecks mit Hilfe der Vektorrechnung und mit Hilfe der elementaren Geometrie. Anschließend vergleichen wir.
Bestimmen der Fläche mit Hilfe der Vektorrechnung
$$ A = \frac{1}{2} \left| \frac{ \overrightarrow{v} } {|\overrightarrow{v}|} \times \overrightarrow{AP} \right | $$ $\overrightarrow{v}$ ist der Richtungsvektor der Geraden. Wenn Sie den Vektor $\overrightarrow{v}$ durch seine Länge teilen, dann hat der Vektor $\overrightarrow{v_0}$ die Länge 1. $$ \overrightarrow{v_0} = \frac{\overrightarrow{v}}{|\overrightarrow{v}|} $$ Da Sie den Richtungsvektor kennen und die beiden Punkte A und P kennen, können Sie die Fläche ausrechnen.
Bestimmen der Fläche mit Hilfe der elementaren Geometrie
Die Fläche A eines Dreiecks: $$ A = \frac{1}{2}\,g h $$ Die Grundsseite ist 1 LE lang: $$ A = \frac{1}{2}\, h $$
Sie können das Vektorprodukt berechnen und da die Fläche in beiden Fällen gleich sein muss, ist die einzige Unbekannte die Länge $\overline{LP}$, bzw. h. Es ergibt sich folgende Formel: $$ d = \frac{ \overrightarrow{v} \times (\overrightarrow{p} - \overrightarrow{a}) }{ |\overrightarrow{v}| } $$
Beispiel
Gesucht ist der minimale Abstand zwischen einem Punkt und einer Geraden. $$ g: \vec{x} = \begin{pmatrix} 13 \\ 12 \\ 7 \end{pmatrix} + t \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} $$ P(2|3|4)
$$ v_0 = \frac{1}{10} \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} $$ $$ A-P = \begin{pmatrix} 13 \\ 12 \\ 7 \end{pmatrix} - \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} = \begin{pmatrix} 11 \\ 9 \\ 3 \end{pmatrix} $$
$$ \begin{array}{rcl} A &=& \left| \frac{1}{10} \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix} \times \begin{pmatrix} 11 \\ 9 \\ 3 \end{pmatrix} \right| \\ &=& \left| \frac{1}{10} \begin{pmatrix} 9 \\ -20 \\ 27 \end{pmatrix} \right| \\ &=& \sqrt{ \frac{ 81 + 400 + 729 } {10 } } \\ &=& \sqrt{ \frac{ 1210 } {10 } } \\ &=& \sqrt{121}\\ &=& 11 \end{array} $$
Beachten Sie, dass Sie den Lotpunkt nicht bestimmt haben und Sie ihn mit dieser Methode auch nicht bestimmen können.