Projektion auf Gerade
Gegeben ist die Gerade g: $$ g: \overrightarrow{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + r \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} = T + r \overrightarrow{b} $$ und der Punkt A(2|5|4). Gesucht ist der Projektionspunkt des Punktes A auf die Gerade g.
Der Richtungsvektor der Geraden g kann normiert werden auf die Länge 1: $$ \left | \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} \right | = 6 $$ $$ g: \overrightarrow{x} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + s \, \frac{1}{6} \, \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} = T + s \, \frac{1}{|\overrightarrow{b}|} \, \overrightarrow{b} $$ Der Parameter s entspricht der Entfernung des Punktes $\overrightarrow{x}$ zu T.
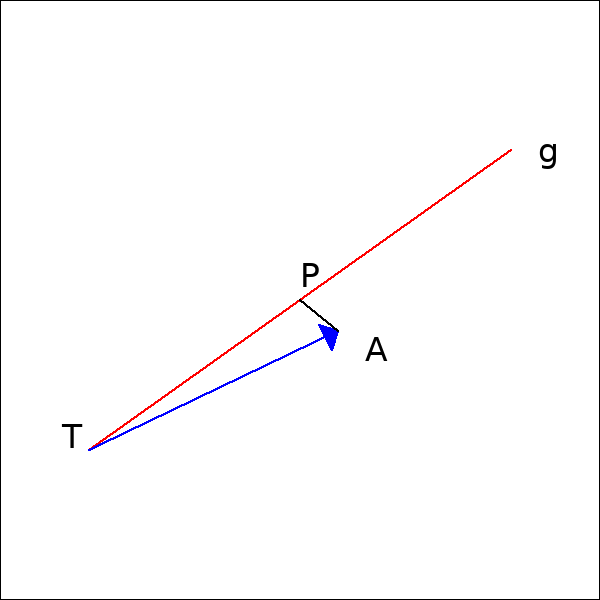
$$ \overrightarrow{TA} \cdot \overrightarrow{b} = |\overrightarrow{TA}| \, |\overrightarrow{b}| \, \cos(\gamma) $$ $\overrightarrow{b}$ ist der Richtungsvektor der Geraden und $\gamma$ der Winkel ATP. $|\overrightarrow{TA}| \, \cos(\gamma)$ ist gleich der Länge der Strecke $\overline{TP}$.
Wenn der Richtungsvektor der Geraden g die Länge eins hat, dann ergibt das Skalarprodukt von $\overrightarrow{TA}$ und dem normierten Richtungsvektor von g die Länge der Strecke $\overline{TP}$.
$$ P = T + \frac{\overrightarrow{TA} \cdot \overrightarrow{b}} {|\overrightarrow{b}|} \, \frac{1}{|\overrightarrow{b}|} \overrightarrow{b} $$
$$ |\overrightarrow{b}| \, |\overrightarrow{b}| = \overrightarrow{b} \cdot \overrightarrow{b} $$ Damit verändert sich die Berechnung noch einmal: $$ P = T + \frac{\overrightarrow{TA} \cdot \overrightarrow{b}} {\overrightarrow{b} \cdot \overrightarrow{b}} \, \overrightarrow{b} $$
In unserem Beispiel bedeutet das: $$ P = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \frac{ \left[ \begin{pmatrix} 2 \\ 5 \\ 4 \end{pmatrix} - \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \right] \cdot \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} }{ \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} } \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} $$ $$ P = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \frac{ \begin{pmatrix} 1 \\ 3 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} }{ 2^2 + 4^2 + 4^2 } \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} $$ $$ P = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \frac{ 2 + 12 + 4 }{ 36 } \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} $$ $$ P = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \frac{ 1 }{ 2 } \begin{pmatrix} 2 \\ 4 \\ 4 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \\ 5 \end{pmatrix} $$

 Koordinatensystem
Koordinatensystem