Hessesche Normalenform (HNF)

Darstellung

Die Hessesche Normalenform ist eine Normalenform, bei der der Normalenvektor die Länge eins hat: $$ E: \left[ \vec{x} - \begin{pmatrix} 1\\2\\3 \end{pmatrix} \right] \cdot \begin{pmatrix} -3 \\ 2 \\ -1 \end{pmatrix} = 0 $$ der Normalenvektor hat die Länge: $$ l = \sqrt {(-3)^2 + 2^2 + (-1)^2} = \sqrt{9+4+1} = \sqrt{14} $$ wird dann zu: $$ E: \left[ \vec{x} - \begin{pmatrix} 1\\2\\3 \end{pmatrix} \right] \cdot \frac{1}{14} \begin{pmatrix} -3 \\ 2 \\ -1 \end{pmatrix} = 0 $$

Abstand zur Ebene

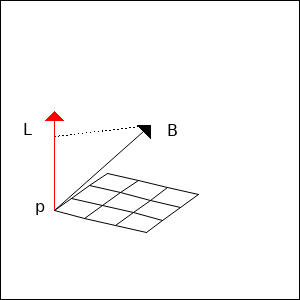
Eine Ebene, ihre Normale und ein Punkt. — Der Normalenvektor (rot) ist senkrecht zur Ebene. Die Projektion von des Punktes P auf die Normale ist gestrichelt gezeichnet. L ist der Projektionspunkt von P auf die Normale. Maxima Code

Die Projektion von B auf die Normale ist gerade der Abstand des Punktes B zur Ebene.
$\gamma$ sei der Winkel zwischen den beiden Vektoren $\overrightarrow{PB}$ und $\overrightarrow{n}$. Das Skalarprodukt der beiden Vektoren $\overrightarrow{PB}$ und $\overrightarrow{n}$ ergibt: $$ \overrightarrow{n} \cdot \overrightarrow{PB} = |\overrightarrow{n}| \, \underbrace{ |\overrightarrow{PB}| \, \cos (\gamma) }_{ |\overline{LP}| } $$
Bei der HNF hat der Normalenvektor die Länge eins: $|\overrightarrow{n}| = 1$. Damit ist das Skalarprodukt gleich der Länge der Strecke von P zu L ($|\overline{LP}|$).
Das Skalarprodukt $\overrightarrow{n} \cdot \overrightarrow{PB}$ berechnen Sie, wenn Sie den Punkt B in die HNF einsetzen.

Beispiel

Gegeben ist die folgende Ebene als HNF: $$ E: \left[ \vec{x} - \begin{pmatrix} 1\\2\\3 \end{pmatrix} \right] \cdot \frac{1}{3} \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} = 0 $$ Bestimmen Sie den Abstand des Punktes E(2|1|3) zu der Ebene. $$ \begin{array}{rcl} d &=& \left[ \begin{pmatrix} 2\\1\\2 \end{pmatrix} - \begin{pmatrix} 1\\2\\3 \end{pmatrix} \right] \cdot \frac{1}{3} \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} \\ &=& \begin{pmatrix} 1\\-1\\-1 \end{pmatrix} \cdot \frac{1}{3} \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} \\ &=& \frac{1 \cdot 2 + (-1) \cdot 1 + (-1) \cdot 2}{3} \\ &=& \frac{2 + (-1) + (-2)}{3} \\ &=& - \frac{1}{3} \end{array} $$ Der Abstand des Punktes E zur Ebene beträgt $\frac{1}{3}$. Die Ebene teilt den Raum in zwei Teile. Die Richtung des Normalenvektors gibt den Teilen jeweils ein positives oder negatives Vorzeichen. Wenn Sie in Richtung des Normalenvektors schauen, dann liegt der Punkt E hinter der Ebene aufgrund des Minuszeichens.