Magische Quadrate: Vorüberlegungen bei (3x3)-Quadraten
Beschriftung
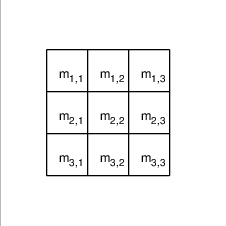
Maxima Code
Die Summe aller Zahlen
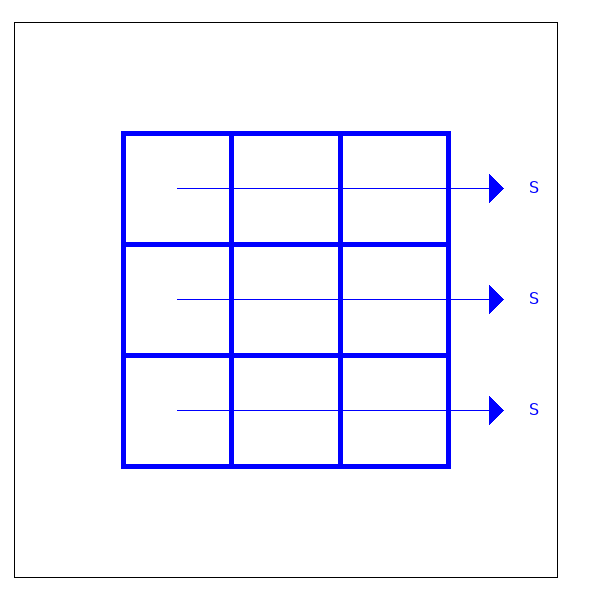
Maxima Code
Jede Zeile hat die Summe S. Es gibt insgesamt drei Zeilen. Also ist die Summe aller Zahlen 3S: $$ m_{1,1} + m_{1,2} + m_{1,3} + m_{2,3} + \ldots = \sum m_{ij} = 3S $$ $m_{ij}$ ist das Element in der i.-ten Zeile und j.-ten Spalte. $\sum$ ist die Summe über alle Elemente.
Das mittlere Element
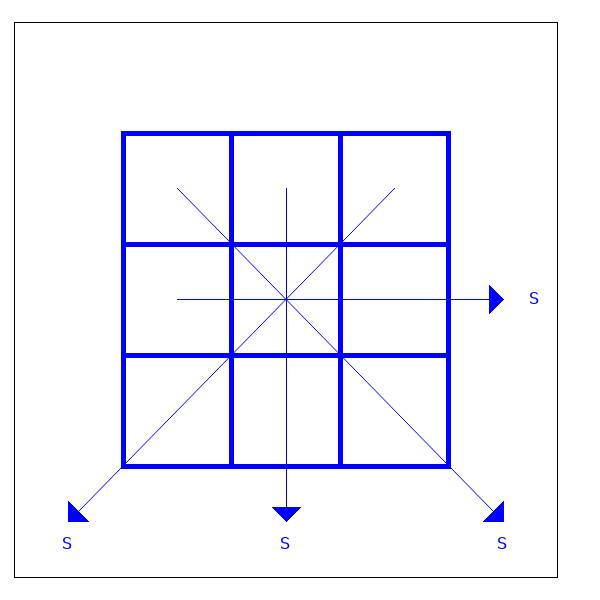
Maxima Code
Die Diagonalen haben die Summe S. Die mittlere Zeile und die mittlere Spalte ebenso. Das mittlere Element wird viermal gezählt.
Diagonale + Diagonale + Spalte und Zeile = $4S$
Die mittlere Spalte, die mittlere Zeile und die beiden
Diagonalen ergeben alle Zahlen genau einmal
bis auf das mittlere Element. Dieses wird jetzt
sogar vierfach gezählt.
$$ \sum m_{ij} + 3 \cdot m_{22} = 4S $$ Die Summe aller Elemente $\left(\sum m_{ij} = 3S \right)$ ist gerade $3 S$. $$ \begin{array}{rcl} 3 S + 3 \cdot m_{22} & = & 4 S \\ 3 \cdot m_{22} & = & S \\ m_{22} & = & \frac{S}{3} \end{array} $$ Das mittlere Element ist gleich der Summenzahl S.
Summe S Magischer (3x3)-Quadrate
Da jede Zahl genau einmal vorkommt und die Summe aller Elemente $3 S$ ergibt gilt: $$ \begin{array}{rcl} \sum m_{ij} & = & 3S \\ 1+2+3+4+5+6+7+8+9 & = & 3S \\ \frac{ (1+9) \cdot 9}{2} & = & 3S \\ 45 & = & 3 S \\ 15 & = & S \end{array} $$Zusammenfassung
$$ \begin{array}{rclcl} S & = & 15 \\ m_{22} & = & \frac{S}{3} & = & 5 \\ \end{array} $$ Insbesondere ist das mittlere Element null, wenn die Summe S null ist.

 Koordinatensystem
Koordinatensystem