Geraden

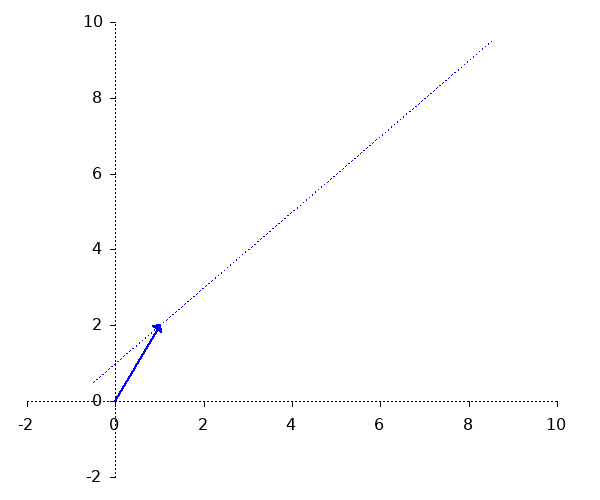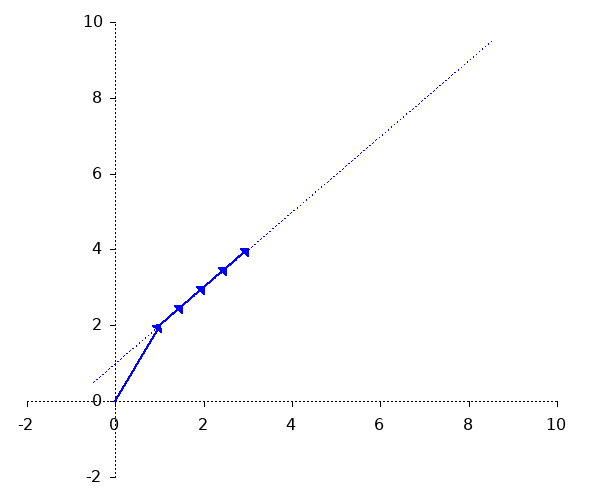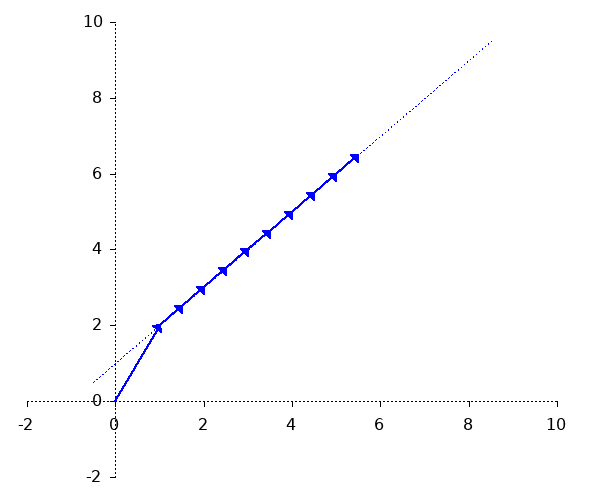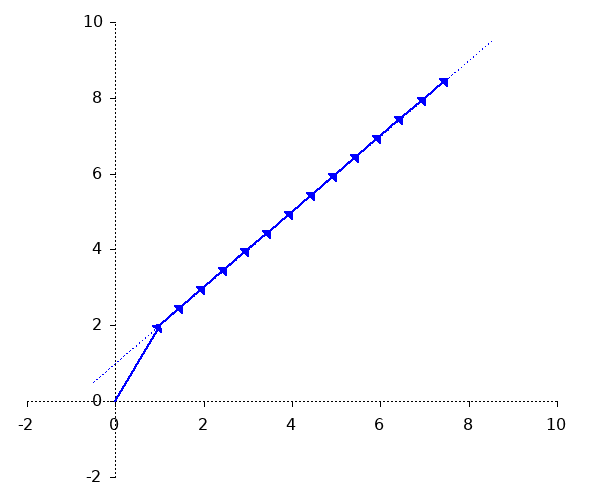
Eine Gerade kann durch einen Punkt A und einen Vektor $c$ und dessen Vielfache dargestellt werden: $$ g: \overrightarrow{x} = A + r \overrightarrow{c} $$

Die Geradengleichung ist folgendermaßen aufgebaut: $$ \underbrace{g}_{\text{Name der Geraden}}: \underbrace{\overrightarrow{x}}_{\text{Punkt der Geraden}} = \underbrace{ \begin{pmatrix} 1 \\ 2 \end{pmatrix} }_{\text{Ein beliebiger Punkt der Geraden}} + t \underbrace{ \begin{pmatrix} 0{,}5 \\ 0{,}5 \end{pmatrix} }_{\text{Richtungsvektor der Geraden}} $$ Eine solche Geradengleichung ist in der Parameterdarstellung. $t$ ist der Parameter, f"ur den Zahlen eingesetzt werden.

Hinweis zum Richtungsvektor

Eine Gerade durch zwei Punkte A und B kann folgendermaßen dargestellt werden: $$ g: \overrightarrow{x} = A + r (B-A) $$ $\overrightarrow{c} = B-A$ ist gerade der Vektor vom Punkt A zu Punkt B. $\overrightarrow{c}$ nennt man den Richtungsvektor. Seine Länge ist nicht entscheidend, sondern nur seine Richtung, denn er wird ja sowieso mit einer Zahl multipliziert. Es empfiehlt sich, als Richtungsvektor einen Vektor zu wählen, der keine Brüche oder Dezimalzahlen enthält und möglichst keine Vielfache: $$ g: \vec{x} = \begin{pmatrix} 1\\2\\ \end{pmatrix} + r \begin{pmatrix} 2\\3\\ \end{pmatrix} $$ $$ h: \vec{x} = \begin{pmatrix} 1\\2 \end{pmatrix} + s \begin{pmatrix} 4\\6 \end{pmatrix} $$ $$ k: \vec{x} = \begin{pmatrix} 1\\2 \end{pmatrix} + t \begin{pmatrix} 1\\1{,}5 \end{pmatrix} $$ Die Geraden g, h und k sind identische Geraden. Die Richtungsvektoren zeigen in dieselbe Richtung, sie sind nur unterschiedlich lang. Jedoch ist g die angenehmste Form.
Beachten Sie, dass Sie nicht ein Vielfaches des Punktes wählen dürfen.