Nachweis eines Quadrates

Gegeben sind vier Punkte im Raum. Weisen Sie nach, dass diese ein Quadrat bilden:
A$(1|1|1)$, B$(5|9|9)$, C$(-3|17|5)$, D$(-7|9|-3)$.

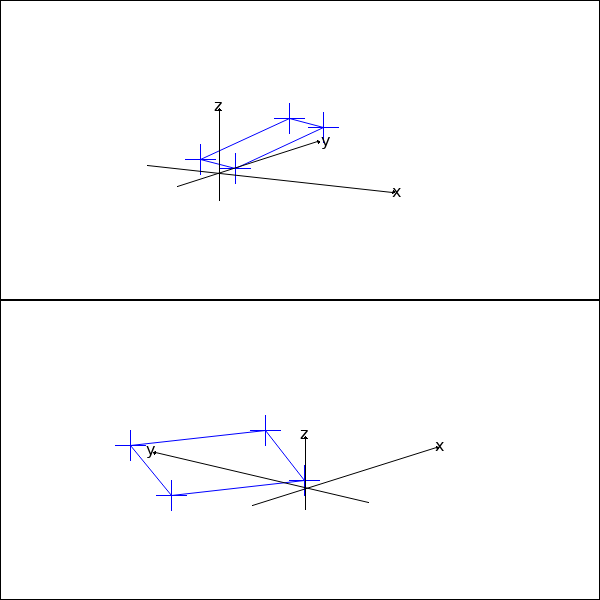
"Ein Viereck ist ein Quadrat, wenn alle Seiten gleichlang sind und einer der Winkel ein 90°-Winkel ist."

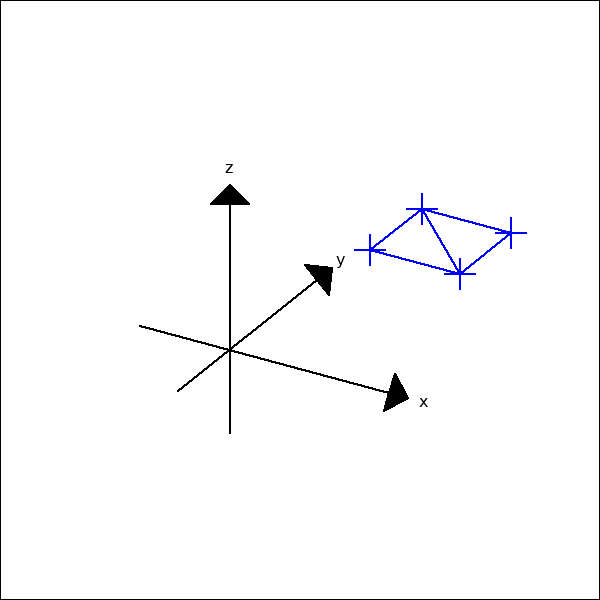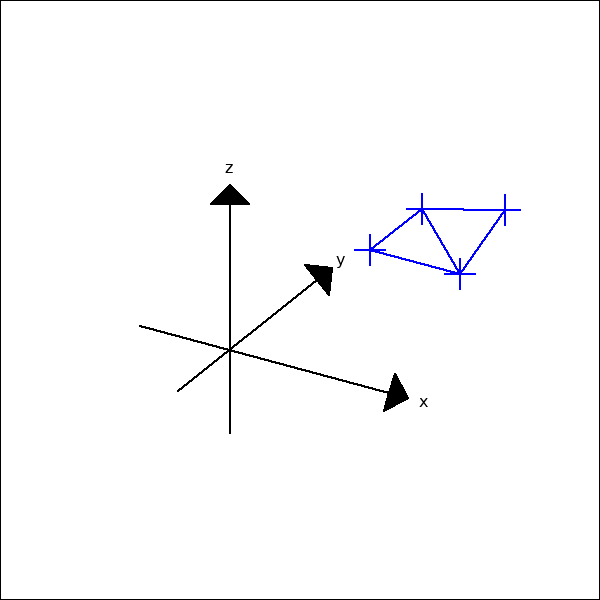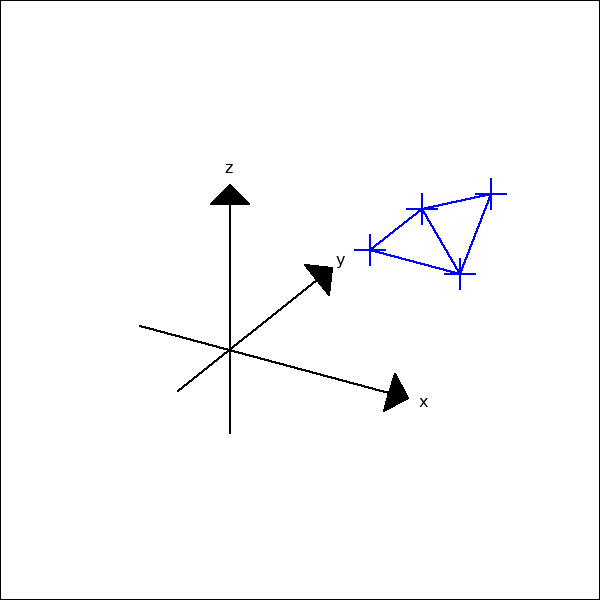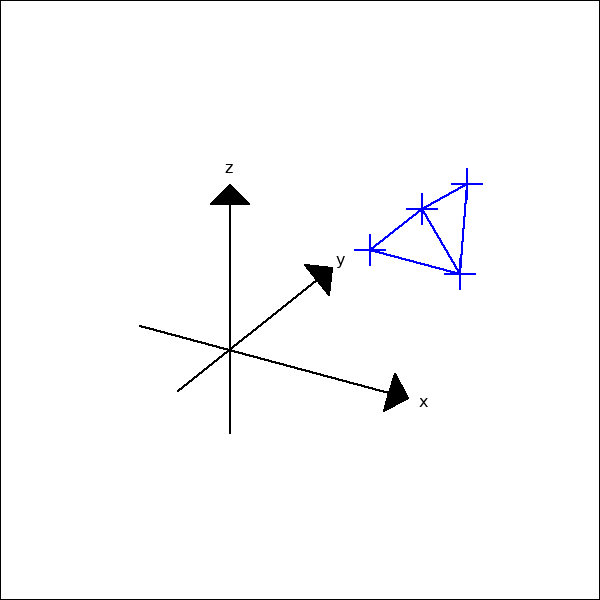
Dieser Ansatz reicht leider im 3-dimensionalen nicht aus wie folgende Animation zeigt. D. h. die 4 Punkte müssen auch in einer Ebene liegen.

Nachweis

Ansatz

Ein Viereck ist ein Quadrat, wenn folgende Bedingungen erfüllt sind:

• Alle Seiten sind gleichlang
• Alle Seiten sind parallel.
• Ein Winkel muss ein 90°-Winkel sein.

Seiten bestimmen

$$ \begin{array}{rccccl} \vec{a} &=& B - A &=& \begin{pmatrix} 5 \\ 9 \\ 9 \end{pmatrix} - \begin{pmatrix} 1\\1\\1 \end{pmatrix} &=& \begin{pmatrix} 4 \\ 8 \\ 8 \end{pmatrix} \\[1ex] \vec{b} &=& C - B &=& \begin{pmatrix} -3 \\ 17 \\ 5 \end{pmatrix} - \begin{pmatrix} 5 \\ 9 \\ 9 \end{pmatrix} &=& \begin{pmatrix} -8 \\ 8 \\ -4 \end{pmatrix} \\[1ex] \vec{c} &=& D - C &=& \begin{pmatrix} -7 \\ 9 \\ -3 \end{pmatrix} - \begin{pmatrix} -3 \\ 17 \\ 5 \end{pmatrix} &=& \begin{pmatrix} -4 \\ -8 \\ -8 \end{pmatrix} \\[1ex] \vec{d} &=& A - D &=& \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} - \begin{pmatrix} -7 \\ 9 \\ -3 \end{pmatrix} &=& \begin{pmatrix} 8 \\ -8 \\ 4 \end{pmatrix} \\[1ex] \end{array} $$

Seiten vergleichen

• $\vec{a}$ und $\vec{c}$ sind gegengleich: $\vec{a} = -\,\vec{c}$ und darum gleichlang.
• $\vec{b}$ und $\vec{d}$ sind ebenfalls gegengleich und darum ebenfalls gleichlang.

Die Seiten sind parallel und gleich lang. Da die Seiten parallel sind, müssen wir jetzt nur einen 90°-Winkel nachweisen.

90°-Winkel nachweisen

$$ \vec{a} \cdot \vec{b} = \begin{pmatrix} 4 \\ 8 \\ 8 \end{pmatrix} \cdot \begin{pmatrix} -8 \\ 8 \\ -4 \end{pmatrix} = 4 \cdot (-8) + 8 \cdot 8 + 8 \cdot (-4) = -32 + 64 - 32 = 0 $$ $\vec{a}$ und $\vec{b}$ schließen einen 90°-Winkel ein.