Das Skalarprodukt -- Überblick

Das Skalarprodukt in der analytischen Geometrie hat wichtige Aufgaben:

• Man kann einen Winkel berechnen.
• Man kann sehr schnell entscheiden, ob ein Winkel ein 90° Winkel ist.
• Man kann sehr einfach einen Vektor mit einem 90° Winkel zu einem anderen Winkel konstruieren.
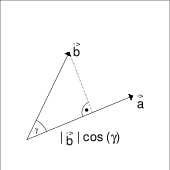
• Man kann die Länge der Projektion berechnen.

Das Skalarprodukt zweier Vektoren wird hier mit Hilfe des eingeschlossenen Winkels definiert: $$\vec{a} \cdot \vec{b} = |\vec{a}| \, |\vec{b}| \, \cos(\gamma)$$

Im Anschauungsraum gilt für das Standardskalarprodukt: $$ \vec{a} \cdot \vec{b} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \end{pmatrix} \cdot \begin{pmatrix} b_1 \\ b_2 \\ \vdots \end{pmatrix} = a_1 \cdot b_1 + a_2 \cdot b_2 \ldots $$ Insbesondere ist das Skalarprodukt eine reelle Zahl.

Besonderheiten

• Wenn der Winkel 90° beträgt, dann ist das Skalarprodukt null, da folgendes gilt: cos(90°) = 0.
  Das ist für den Nachweis eines 90° Winkels, bzw. der Orthogonalität, sehr hilfreich.
• $\vec{a} \cdot \vec{a} = |\vec{a}|^2$, da cos(0) = 1 gilt. Insbesondere ist $\vec{a} \cdot \vec{a}$ gleich dem Quadrat der Länge des Vektors $\vec{a}$.