Multiplizieren zweier Brüche

Multiplizieren eines einfachen Bruches mit einem Bruch

Wir beginnen wieder mit einem Beispiel.
Wieviel ist $ \frac{1}{3} \cdot \frac{3}{4} $ ?
Oder: Wieviel ist ein Drittel von $\frac{3}{4} $ ?

Die $\frac{3}{4}$ müssen durch drei geteilt werden.
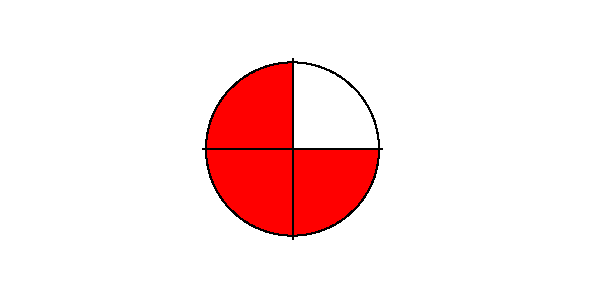
Da der Bruchstrich im Prinzip ein Geteiltzeichen ist: $$ \frac{1}{3} \cdot \frac{3}{4} = \frac{3}{3 \cdot 4} = \frac{1}{4} $$ Beim Multiplizieren eines Bruches mit einem anderen Bruch werden die Nenner miteinander multipliziert.

Multiplizieren eines Bruches mit einem Bruch

Ein Beispiel:
Wieviel ist $ \frac{2}{3} \cdot \frac{3}{4} $ ?
Oder: Wieviel sind zwei Drittel von $\frac{3}{4} $ ?

Die $\frac{3}{4}$ müssen durch drei geteilt werden und mit zwei multipliziert werden:. $$ \frac{2}{3} \cdot \frac{3}{4} = 2 \cdot \frac{1}{3} \cdot \frac{3}{4} = 2 \cdot \frac{3}{3 \cdot 4} = \frac{2 \cdot 3}{3 \cdot 4} = \frac{2}{4} = \frac{1}{2} $$ Beim Multiplizieren eines Bruches mit einem anderen Bruch werden die Nenner miteinander multipliziert und die Zähler werden miteinander multipliziert..

Multiplizieren zweier beliebiger Brüche

Die Merkregel vereinfacht das Rechnen mit Brüchen. Man schreibt die Zähler und die Nenner mit dem Multiplikationszeichen auf und dann kürzt man: $$ \frac{3}{4} \cdot \frac{5}{2} = \frac{3 \cdot 5}{4 \cdot 2} = \frac{15}{8}$$ Warum ist das so?

• Zuerst wird der Bruch $\frac{5}{2}$ in vier gleiche Teile geteilt. Dazu wird die Unterteilung vier mal so fein gemacht: $$\frac{5}{2} : 4 = \frac{5}{8}$$
• Anschliessend werden die $\frac{5}{8}$ mit drei multipliziert.

Weiteres Beispiel: $$ \frac{3}{4} \cdot \frac{2}{3} = \frac{3 \cdot 2}{4 \cdot 3} $$ erst kürzen ergibt: $ \require{cancel}$ $$ = \frac{\cancel{3} \cdot 2}{4 \cdot \cancel{3}} = \frac{2}{4}$$ mit $4 = 2 \cdot 2$ ergibt sich: $$ = \frac{\cancel{2}}{2 \cdot \cancel{2} } $$ $$ = \frac{1}{2} $$