Multiplizieren

Multiplizieren eines Bruches mit einer ganzen Zahl

Wir beginnen wieder mit einem Beispiel: $$ \frac{3}{4} \cdot 2 = ? $$

Aspekt: Häufigkeit

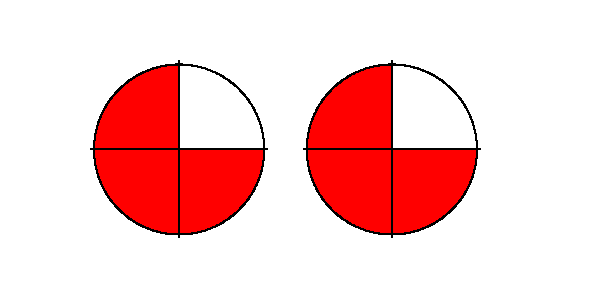
graphisch: 2 * 3/4 = 6/4
Das Doppelte von $\frac{3}{4}$ sind $\frac{6}{4} = \frac{3}{2}$ Maxima Code
Wir erkennen, dass man einen Bruch mit einer Zahl multipliziert, in dem man den Nenner beibehält und nur den Zähler mit der Zahl multipliziert. $$ \frac{3}{4} \cdot 2 = \frac{3}{4} + \frac{3}{4} = \frac{3 + 3}{4} = \frac{3 \cdot 2}{4} = \frac{6}{4} $$

Aspekt: Anteil

Hier zielt der Aspekt ab auf die Frage wie viel $\frac{3}{4}$ von 2 ist.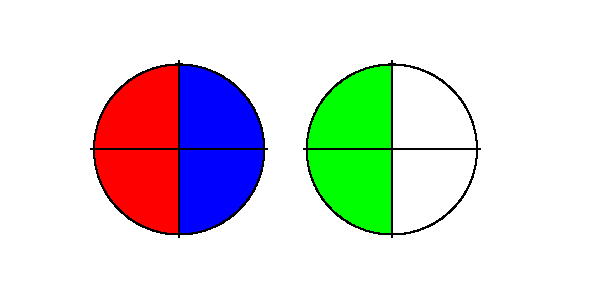
graphisch: 3/4 von 2 = 6/4
$\frac{3}{4}$ von zwei Kreisen sind $\frac{6}{4} = \frac{3}{2}$ Maxima Code
  1. Dazu werden die 2 Kreise in vier gleiche Teile eingeteilt: rot, blau. grün und weiss.
  2. Ein Viertel der beiden Kreise ist jeweils ein Halbkreis
  3. Drei Viertel sind dann z. B. die rote und die blaue und die grüne Fläche zusammen.
  4. $\frac{3}{4} \cdot 2 = 3 \cdot \frac{1}{2} = \frac{3}{2}$

    5. $\frac{3}{4} \cdot 2 = 3 \cdot \frac{2}{4} = 3 \cdot \frac{1}{2} = \frac{6}{4}$