Dividieren - grafische Beispiele

Dividieren einer ganzen Zahl durch einen Bruch

Wir beginnen wieder mit einem Beispiel:

• Wie oft passt $\frac{1}{4}$ in 2?
• Sie haben 2 Torten, wieviele Viertel-Stücke können Sie verteilen?

$$ 2 : \frac{1}{4} = \, ? $$

$$ \begin{align*} 2 : \frac{1}{4} &= \frac{2 \cdot 4}{4} : \frac{1}{4}\\ &= \frac{8}{4} : \frac{1}{4}\\ &= 8 \end{align*} $$

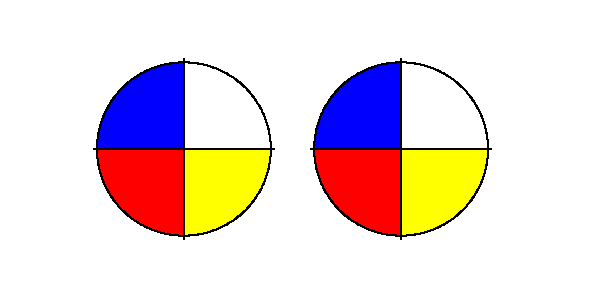
Wenn die Nenner gleich sind, dann reicht es einfach nur die beiden Zähler zu dividieren.

Dividieren eines Bruches durch einen Bruch

Wir untersuchen zuerst eine Fragestellung, bei der das Ergebnis eine ganze Zahl ist.

Sie haben einen halben Kuchen übrig. Wie viele Viertel-Stücke können Sie verteilen?

$$ \begin{align*} \frac{1}{2} : \frac{1}{4} &= \frac{2}{4} : \frac{1}{4} \\ &= 2 \end{align*} $$ Auch hier erweitern wir auf denselben Nenner. Wir werden auf der nächsten Seite sehen, wie man das ganz einfach machen kann.

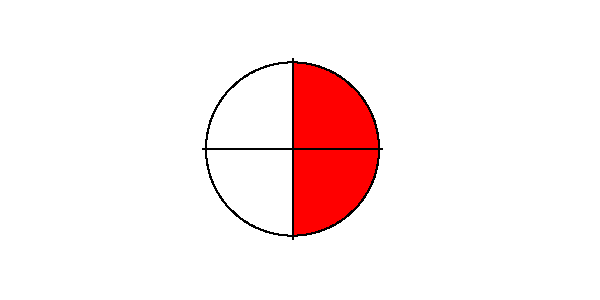
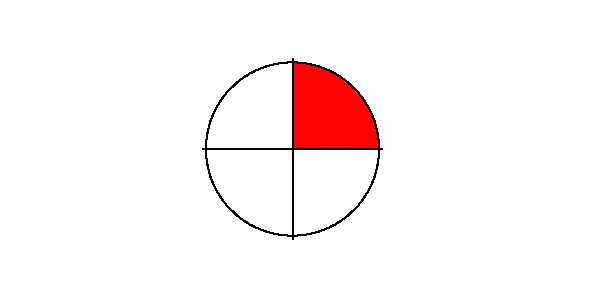
Wie ist das denn, wenn das Ergebnis nicht ganzzahlig ist? Also, wie oft passen $\frac{3}{4}$ in $\frac{1}{2}$?

Der 3/4-Kreis passt nur zu 2/3 in den halben Kreis:\\ Wir erweitern kreuzweise, um dieselben Nenner zu erhalten: $$ \begin{align*} \frac{1}{\color{blue}{2}} : \frac{3}{\color{red}{4}} &= \frac{1 \cdot \color{red}{4}}{\color{blue} {2} \cdot \color{red}{4}} : \frac{3 \cdot \color{blue}{2}} {\color{red}{4} \cdot \color{blue}{2}} // &= \frac{4}{8} : \frac{6}{8} \\ &= \frac{4}{6} \\ &= \frac{2}{3} \end{align*} $$ Beachten Sie, dass wir den gemeinsamen Nenner aber eigentlich gar nicht benötigen.

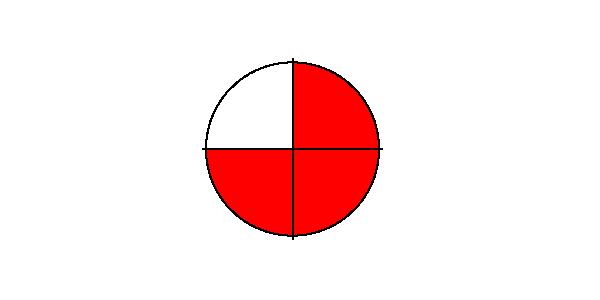
Kürzer ist folgende Rechnung: $$ \begin{align*} \frac{1}{2} : \frac{3}{4} &= \frac{1 \cdot 4}{2 \cdot 3} \\ &= \frac{4}{6} \\ &= \frac{2}{3} \end{align*} $$