Addieren

Addieren zweier Brüche mit demselben Nenner

Wir beginnen mit Beispielen:
graphisch: 1/4 + 1/4 = 2/4
$\frac{1}{4} + \frac{1}{4} = \frac{2}{4} = \frac{1}{2}$
graphisch: 1/3 + 1/3 = 2/3
$\frac{1}{3} + \frac{1}{3} = \frac{2}{3} $
Wenn zwei Brüche denselben Nenner haben, dann sind die Unterteilungen gleich. Dann kann man einfach die Zähler addieren.

Addieren zweier Brüche mit verschiedenen Nenner

Wie erhält man die Lösung von z. B.: $\frac{1}{2} + \frac{1}{3}$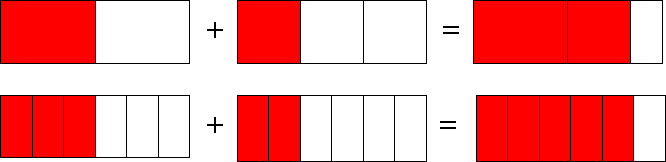
graphisch: 1/2 + 1/3 = 5/6
Man muss zuerst Erweitern (gleiche Unterteilung herstellen:) $ \frac{1}{2} = \frac{3}{6} \;\;\;\; \frac{1}{3} = \frac{2}{6} $
Mit diesem Wissen können wir dann addieren: $$ \frac{1}{2} + \frac{1}{3} = \frac{3}{6} + \frac{2}{6} = \frac{5}{6} $$

Merkregel:
Um zwei Brüche mit verschiedenen Nenner zu addieren (subtrahieren) muss man zuerst beide Brüche auf denselben Nenner erweitern.