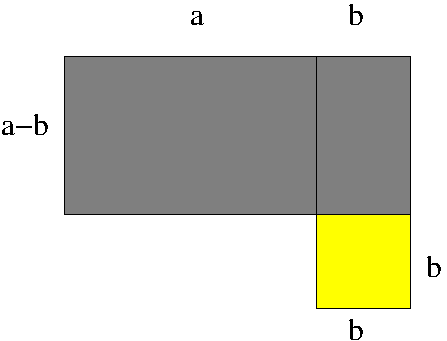
Diesmal verändern wir nicht die Figur sondern färben sie anders ein.
Das graue Rechteck hat die Fläche $(a-b)(a+b)$
Das gelbe Quadrat hat die Seitenlänge $b$ und ist damit $b^2$ groß.

Das graue Rechteck und das gelbe Quadrat haben immer noch zusammen die Fläche $a^2$, da wir nichts weggenommen haben sondern nur die Flächen zerschnitten und anders angeordnet haben.
Die graue Fläche ist die Fläche des Ausgangsquadrates minus der Fläche des gelben Quadrates: $$ (a-b)(a+b) = a^2 - b^2 $$ Dies ist gerade die 3. Binomische Formel.
Übersicht: Beweise