
Die Annahme: Die Wurzel von 2 sei ein Bruch.
Beweis der Irrationalität von Wurzel 2
Bringen Sie die Bilder auf der linken
Seite in die richtige Reihenfolge.
In der richtigen Reihenfolge ergibt sich der
Beweis, dass Wurzel aus 2 nicht als Bruch zweier
natürlicher Zahlen darstellbar ist.
Der Beweis erfolgt durch einen Widerspruch zur Annahme.

Die Annahme: Die Wurzel von 2 sei ein Bruch.

Quadrieren beider Seiten.
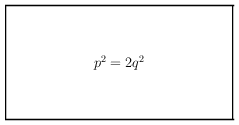
2q2 ist gerade, also auch 2p2
Das Produkt zweier ungeraden Zahlen ist ungerade. Also kann p nur gerade sein, Es gibt also eine Zahl r mit 2 ⋅ r = p. Beispiel: 6 = 2 ⋅ 3, 8 = 2 ⋅ 4 usw.

also ist auch q2 gerade und damit q.

p und q sind gerade dass ist ein Widerspruch zur Annahme.
Also ist die Annahme falsch. Die Wurzel von 2 ist nicht durch einen Bruch darstellbar.